Transformer Model Architecture

From encoders to masked attention and decoders - Transformer architecture demystified.

Part of the Transformers & Attention series.

The Fig.1 given below is showing a Transformer Model Architecture as per the paper ā€œAttention Is All You Needā€ published in 2017 by A. Vaswani et al. It has two blocks - the left block is Encoder and the right block is Decoder. This transformer-based encoder-decoder architecture operates similarly to the RNN-based encoder-decoder that we saw in the previous translation example but without the presence of an RNN component. Despite this difference, the input-output feeding mechanism to the encoder-decoder remains consistent. Additionally, akin to the RNN model, the decoder functions as a causal model.

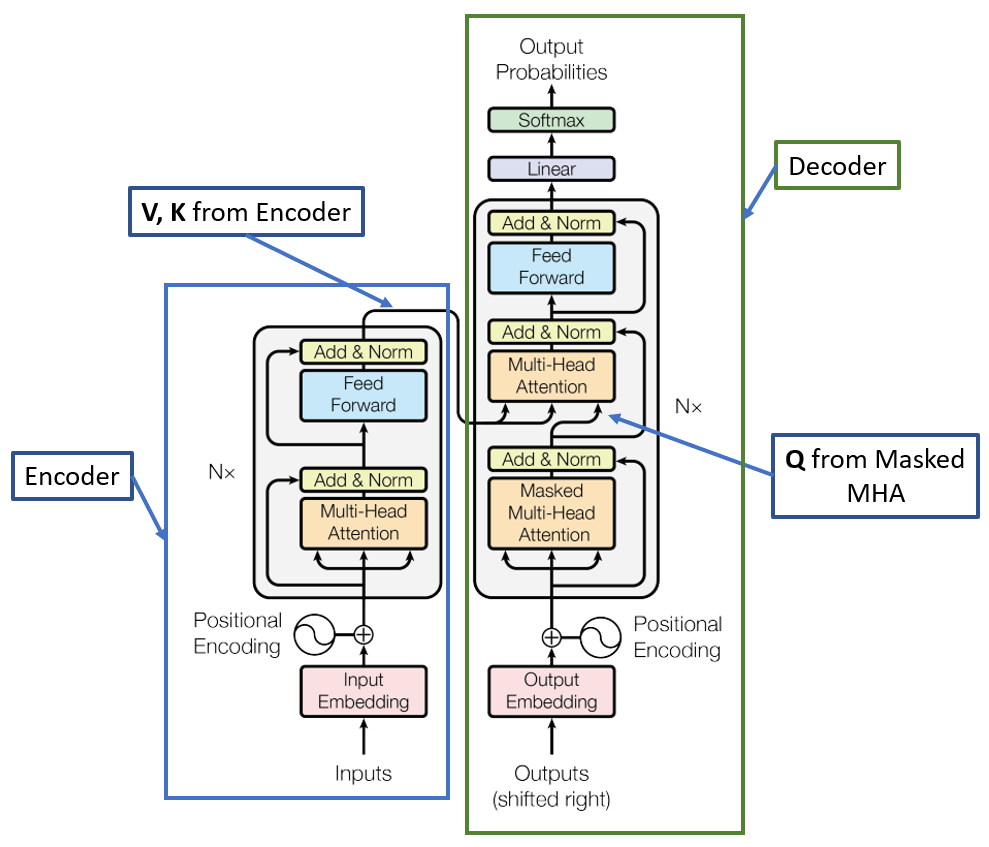
Figure 1

Figure 1

The encoder sends Values(V) and Queries(Q) to the decoder, linking them together to create the entire Transformer system. This connection, known as cross-attention, enables the decoder to pay attention to the encoded information from the input sequence provided by the encoder. With this mechanism, the decoder can concentrate on different sections of the input sequence when producing the output sequence.

It's important to understand that the encoder and decoder components can function independently as standalone models for various tasks. For instance, BERT serves as an exclusive encoder architecture, while GPT operates solely as a decoder architecture. On the other hand, T5 incorporates both encoder and decoder components within its architecture.

The Encoder and Decoder blocks share similar components, including Positional Encoding, Multi-Head Attention, Add & Norm (comprising Skip connection and Layer normalization), and Feed Forward. However, one thing to notice is that as the decoder functions as a causal model, it employs causal attention or masked attention. This means that each token is restricted to attending only to its preceding tokens, not the subsequent ones.

Mastering the Encoder block facilitates comprehension of the Decoder block and the entire Transformer architecture. Letā€™s see Encoder in detail.

Encoder

The Encoder consists of transformer block as shown in Fig. 2. A simplified and expanded diagram is also shown on the right side. Letā€™s understand the internal components of a Transformer block.

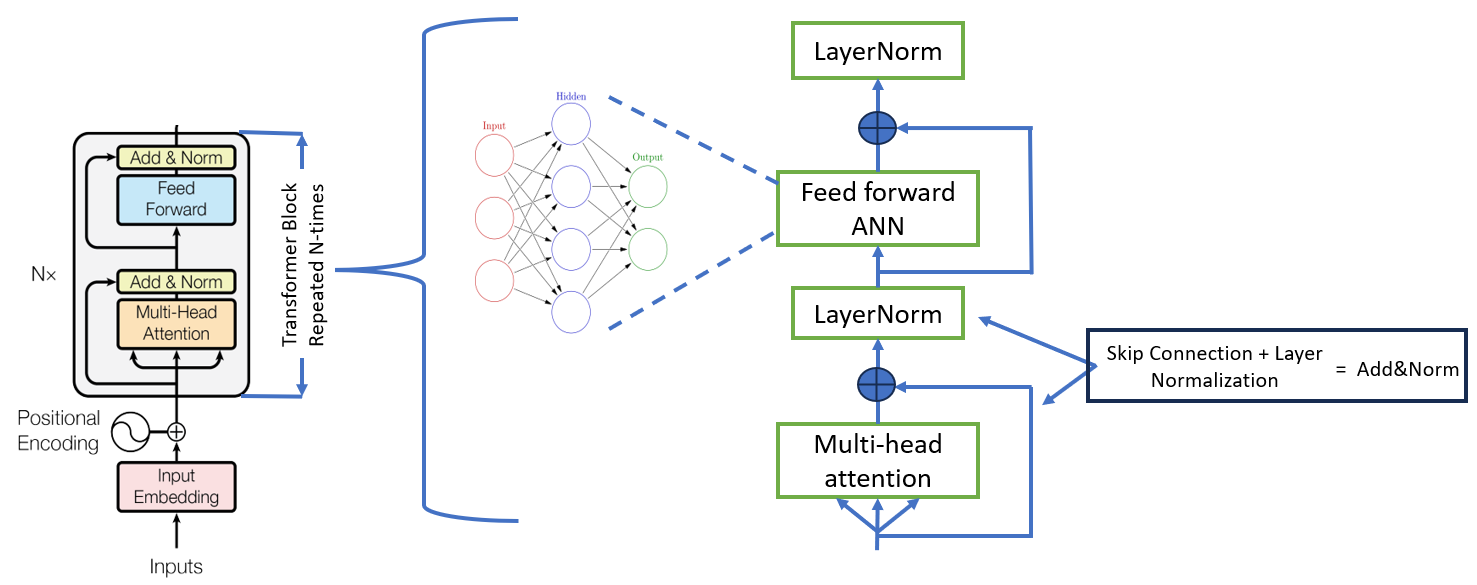
Figure 2

Figure 2

The Transformer block can be sub-divided into two main sub-layers:

  • The first sub-layer comprises a multi-head attention mechanism that receives the queries, keys, and values as inputs.
  • A second sub-layer comprises a fully-connected feed-forward network.

Following each of these two sub-layers is layer normalization, into which the sub-layer input (through a residual/skip connection) and output are fed. Regularization is also introduced into the model by applying a dropout to the output of each sub-layer (before the layer normalization step) which is not shown in the figure.

The feed-forward network allows the model to extract higher-level features from the input. This network usually comprises two linear layers with a ReLU activation function in between. The feed-forward network allows the model to extract deeper meaning from the input data and more compactly and usefully represent the input. In the paper, an ANN with one hidden layer and a ReLu activation in the middle with no activation function at output layer has been implemented.

Encoder is formed by repeated transformer block joined one after another multiple times which is shown as multiplied by N in Fig.2 above. The transformer encoder is a crucial part of the transformer encoder-decoder architecture, which is widely used for natural language processing tasks.

BERT which stands for Bi-directional encoder representation is an encoder-only architecture that consists of 6 to 12 such transformer blocks and a prediction head as the last layer, shown in Fig.3 below.

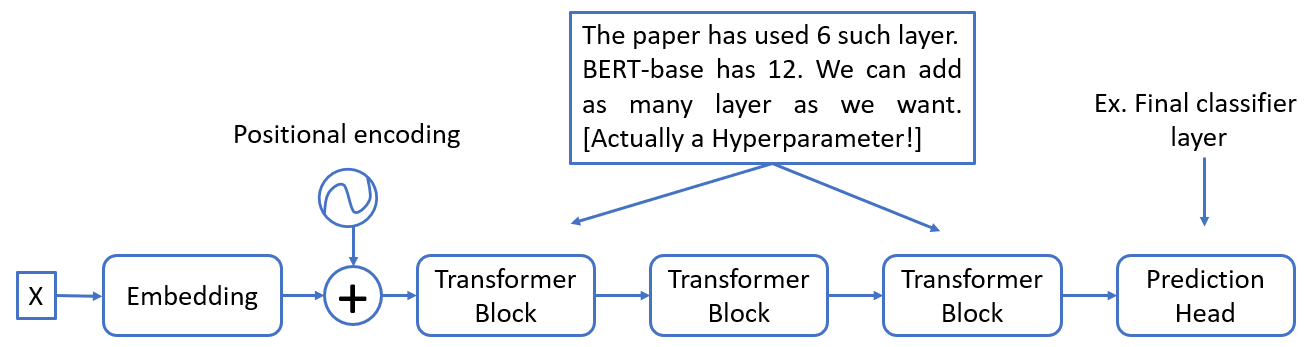
Figure 3

Figure 3

Multi-Head Attention

Please go through the previous article on the Self-Attention mechanism, which has implemented in Multi-Head Attention. In Multi-Head Attention, the Attention module repeats its computations multiple times in parallel. Each of these is called an Attention Head.The Attention module splits its Query, Key, and Value parameters N-ways and passes each split independently through a separate Head. All of these similar Attention calculations are then combined to produce a final Attention score. This is called multi-head attention and gives the Transformer greater power to encode multiple relationships and nuances for each word. A schematic representation of MHA is shown in Fig.4 below.

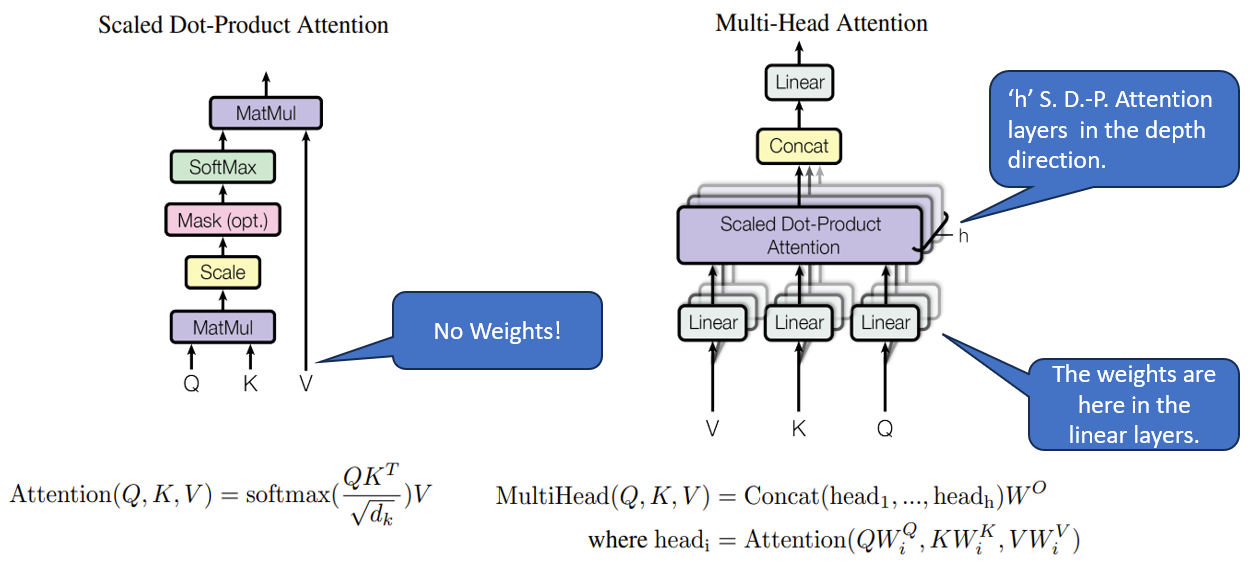
Figure 4

Figure 4

Shape tracking and related calculations are shown with the help of Fig. 5.

  • The shape of input to each self-attention layer \( \rightarrow (T \times d_{model})\)
  • The output shape after each attention layer \( \rightarrow (T \times d_{V})\)
  • After concatenation the shape of output [concatenate them along the feature dimension] \( \rightarrow(T \times hd_{V})\)

Imagine that output of each self-attention block lined up side by side after concatenation.

Final Projection: Output = Concat \((A_1, A_2, ā€¦, A_h ) W^O\)

  • Shape of : Concat \((A_1, A_2, ā€¦, A_h ) \rightarrow (T \times hd_{V})\)
  • Shape of : \( W^O \rightarrow (hd_V \times d_{model} )\)
  • Shape of final Output = Concat \((A_1, A_2, ā€¦, A_h ) W^O\)
    \(= (T \times hd_V) \times (hd_V \times d_{model} ) \rightarrow(T \times d_{model} )\)
    Back to the initial input shape!
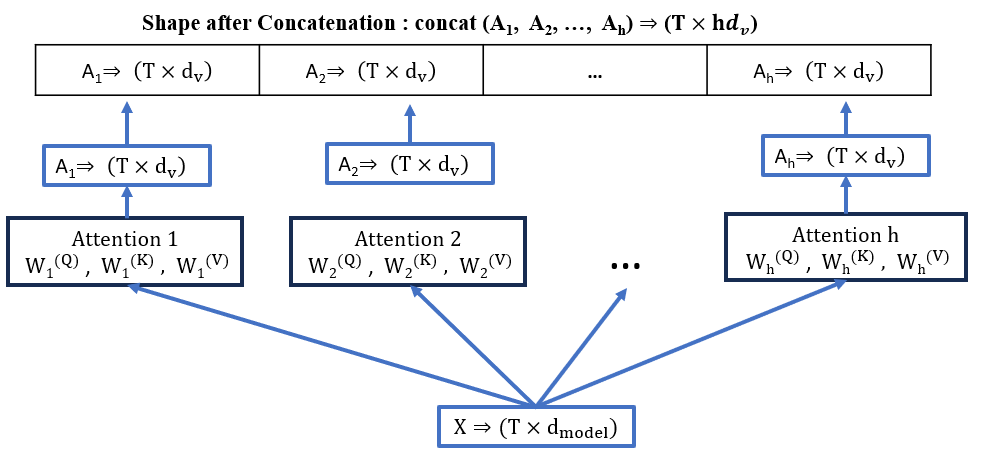
Figure 5

Figure 5

We can notice in the above figure that each attention calculation is functioning parallelly and has no dependency on the other.

Positional Encoding

Passing embeddings directly into the transformer block results in missing of information about the order of tokens as we get rid of RNN blocks and attention is permutation invariant i.e. order of token does not matter to attention.

Although transformers are a sequence model, it appears that this important detail has somehow been lost. Positional encoding is for rescue. Positional encoding adds positional information to the existing embeddings.

A unique set of numbers added at each position of the existing embeddings, such that this new set of numbers can uniquely identify which position they are located at.

Following two ways are there to add positional encoding:

  1. Positional Encoding by Sub-Classing the Embedding Layer (Trainable)
  2. Positional Encoding scheme as per the paper (non-trainable)

In the scheme suggested in the paper the encoding is created by using a set of sins and cosines at different frequencies. The paper uses the following formula for calculating the positional encoding.

\( PE_{(pos,\,2i)}=\sin\!\left(\frac{pos}{10000^{2i/d_{model}}}\right) \)

\( PE_{(pos,\,2i+1)}=\cos\!\left(\frac{pos}{10000^{2i/d_{model}}}\right) \)

Causal Attention/Masked Attention in Decoder Block

All the above-mentioned components are found in both the encoder and decoder blocks. However, the decoder block utilizes a Causal Attention/Masked Attention Mechanism, differing slightly from the Attention mechanism in the encoder block. Let's explore further.

Decoder is a causal model i.e. it acts like a text generation tool, similar to how forecasts are made in time series analysis, where it predicts the next element based on previous ones. To accomplish this, when generating output at any position in the sequence, the model should only be permitted to consider the preceding tokens, excluding any tokens that followed.

Let's see mathematically how to achieve this through an attention score matrix. The Fig.6(a) below shows the attention score matrix for just 5 tokens for the sake of demonstration. It will have a shape of \(T \times T \) for \(T\) sequences. Here, the attention score \(Ī± (i, j)\) represents how much "(\i\)" pays attention to "\(j\)".

Is it possible to restrict attention weights to consider only past input tokens? Yes, through some manipulation, we can achieve this: \( Ī± (i, j) > 0 \) only when \(i > =j\), resulting in the score matrix depicted in Fig.6(b).

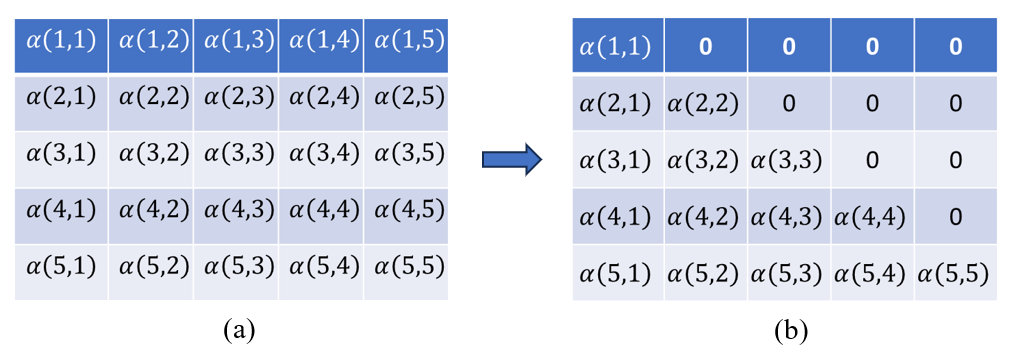
Figure 6

Figure 6

We have masked the upper triangular elements to set them to zero. Thus, rather than employing plain Multi-Head Attention, we utilize a masked version known as 'Causal Self-Attention.

Finally, the Decoder is depicted in Fig. 7 below, which is equivalent to the Encoder, but the transformer block implements Masked Multi-Head Attention. All GPTs(Generative Pre-trained Transformers) are versions of decoder-only architecture with many more components attached to them, trained on a humongous amount of data.

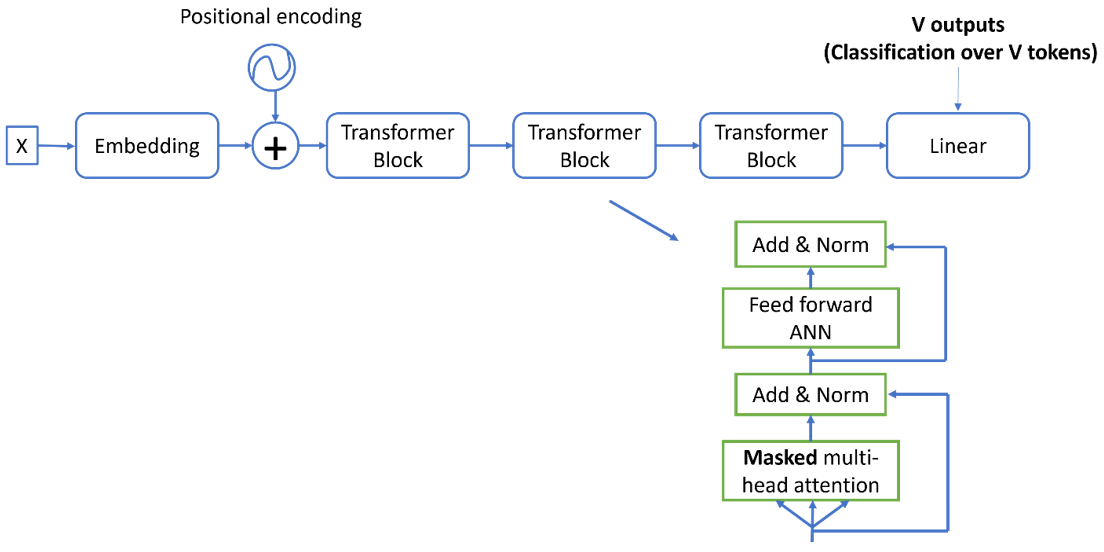
Figure 7

Figure 7

We have seen both the Encoder and Decoder separately. Encoder-only architecture is BERT while Decoder-only Architecture is GPT. Similarly, the architecture that contains both Encoder and Decoder is called T5 i.e. `Text to Text Transfer Transformerā€™. The Fig. 8 below shows how Encoder and Decoder are connected in full Encoder and Decoder architecture.

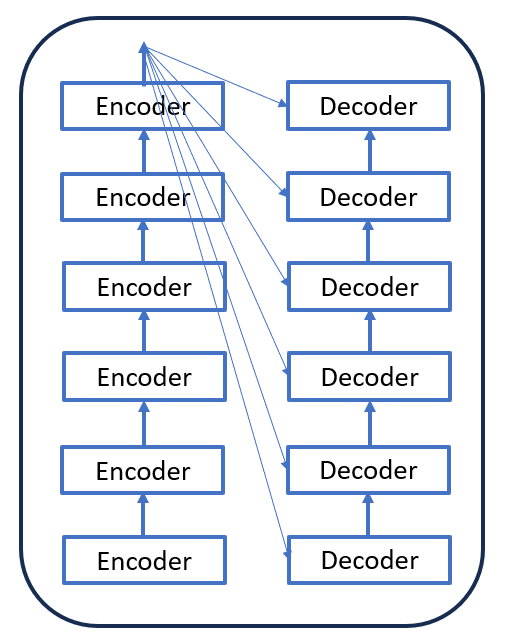
Figure 8

Figure 8

Why does multi-head attention work?

It allows the layer to learn multiple features. Think of attention outputs as features that tell us something about the sentence. For example, see the Fig. 9 below, when Suman pays attention to bank, the feature might be Where did Suman go? But we might also be interested in what Suman did. He cashed the check. We can only do this if we allow our layer to produce multiple features, each of which has the Suman token pay attention to different tokens in the sentence. There would be multiple and different kind of relationship and dependency between different tokens in any sequence. Multi-head attention helps in learning those different relationships by learning corresponding multiple features.

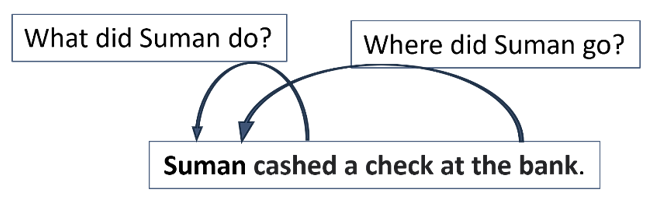
Figure 9

Figure 9